Markov Decision Process (MDP): The Foundation of RL
Machine learning employs reinforcement learning (RL) as a strong paradigm which allows agents to optimize their decisions through environmental experience. The mathematical core of decision-making problems in RL exists within the Markov Decision Process (MDP) framework. MDPs establish the fundamental framework in reinforcement learning which makes them essential knowledge for anyone working with this field.
This complete article delves into Markov Decision Process (MDP) examination through definitions, explanations of elements, properties, real-world implementations and crucial standing in reinforcement learning algorithms. The article examines both implementation challenges as well as MDP extensions alongside their practical applications.
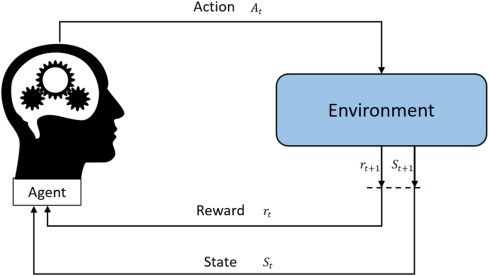
What is a Markov Decision Process (MDP)?
A Markov Decision Process (MDP) serves as a mathematical system that handles decision sequences which combine random environmental effects with actions from the decision-making entity. Through its structure an agent can generate decisions that optimize the total reward accumulation throughout an ongoing period.
Under the MDP framework all environmental dynamics and agent behaviors alongside task objectives combine in an organized manner. An MDP assumption of Markovian characteristics states that the future state becomes defined by the existing state and present action while disregarding previous sequence occurrences.
Components of a Markov Decision Process
A Markov Decision Process consists of the 5-tuple elements S, A, P, R, γ.
- S (States): A MDP features S (States) as the complete collection of states available to the agent when existing. At any specific time a state presents an environmental depiction.
- A (Actions): A represents all actions which an agent has the capability to perform. The action that an agent chooses will determine the following state it enters into.
- P (Transition Probability Function): This function describes the chance of moving between states s’ and s when the agent carries out action a which is displayed as P(s’ | s, a). The environment’s operational rules are contained within this specification.
R (Reward Function): Rephrase The Reward Function provides numerical rewards (R(s,a,s’)) that result when an agent moves between states while
- executing action ‘a’. Agent learning gets directed by rewards which serve as problem-solving indications.
- γ (Discount Factor): The variable γ serves as the discount factor that ranges from 0 to 1 so agents can weight present rewards against upcoming rewards. The value of γ determines whether the system prioritizes immediate rewards over future ones where higher values prefer long-term rewards.
The Markov Property
The core idea of MDPs rests on the implementation of the Markov Property. The transition probabilities depend upon the current state and action alone so that past state-action sequences have no influence.
P(s_{t+1} | s_t, a_t) = P(s_{t+1} | s_1, a_1, …, s_t, a_t)
Due to this property MDPs become an effective and manageable framework for decision problems.
Policy, Value Functions, and Objective
Within MDP the agent strives to discover a maximum reward cumulative policy that guides their actions for extended durations. The application of following achievement methods enables this process:
- Policy (π): A policy designates actions through states with its mathematical representation as π(s). In each state the agent embraces actions based on policy’s definition.
- Value Function (V): The expected return starting from state s and following policy π thereafter is calculated by the value function V(s).
- Action-Value Function (Q): The Q-function provides Q(s,a) to evaluate the expected return that occurs during state’s when the agent uses action a and continues under policy π.
- Objective: An agent identifies π* by selecting a policy that achieves maximum rewards from every state.
V(s) = max_π E[∑γ^t R(s_t, a_t)]*
Solving an MDP
The MDP solution involves various procedures to discover the best policy π* of optimal actions.
- Dynamic Programming (DP): DP methodologies operate through designing recursive procedures for value iteration and policy iteration when one possesses knowledge about P and R.
- Monte Carlo Methods: The estimation of value functions through sample episode collection becomes viable when the model is unavailable during Monte Carlo Methods.
- Temporal Difference (TD) Learning: Temporal Difference (TD) Learning combines Dynamic Programming and Monte Carlo methods through which it uses past estimates to update value predictions during bootstrapping.
- Q-Learning and SARSA: The Q-Learning method belongs to the model-free category while being off-policy whereas SARSA acts as a model-free and on-policy approach which learns the Q-values independently from transition probability knowledge.
Example: Grid world MDP
In this scenario an agent uses cells from a grid to represent states as it proceeds. The agent possesses four movement options between adjacent locations including upward and downward movement as well as left and right movement. The agent receives a reward upon reaching its goal position but incurs a negative reward when encountering obstacles.
- States: Grid positions (x, y)
- Actions: {Up, Down, Left, Right}
- Transition: Deterministic or probabilistic moves
- Reward: The rewards for this MDP model are +1 points for reaching the goal and -1 points for obstacles but all other actions result in zero reward.
The solution from this MDP enables the agent to discover the most suitable path to the target destination.
Applications of MDPs in Real Life
Markov Decision Processes serve practical uses in numerous real-life applications along with their theoretical significance:
- Healthcare: Personalized treatment strategies and resource allocation in hospitals.
- Finance: The financial sector uses MDP models both for optimal portfolio adjustments and risk reduction logic.
- Gaming: AI strategies in board games and video games (e.g., AlphaGo).
- Operations Research: Operations Research makes use of MDPs to optimize inventory management and supply chains while designing queuing systems.
- Autonomous Vehicles: Self-Driven Vehicles Utilize MDP-Based Decision Systems for Mapping Routes and Detecting Hazards Together with Command System Operations.
Limitations of the MDP Framework
- State Explosion: Complex environments produce state expansion problems which increase the number of possible states exponentially.
- Model Dependency: Many solutions based on MDPs require information related to transition probabilities and reward functions for successful operation.
- Markov Assumption: The future photographed by the Markov Assumption exists independently from previous occurrences in real-world situations.
Extensions of MDPs
Several academic researchers have created different expanded versions to address these MDP limitations.
- Partially Observable MDPs (POMDPs): Organizations implementing Partially Observable MDPs (POMDPs) can process systems with agents who lack complete state awareness.
- Semi-Markov Decision Processes (SMDPs): Semi-Markov Decision Processes (SMDPs) extend MDPs by enabling the modeling of procedures that require distinct amounts of time duration.
- Hierarchical MDPs (HMDPs): Hierarchical MDPs accept complex tasks by dividing them into smaller subtasks to streamline learning progress.
- Multi-Agent MDPs: The Multi-Agent MDP framework models environments that include two or more agents which interact within them.
MDPs in Reinforcement Learning
The environment being modeled as MDP represents one of the standard elements in reinforcement learning systems. Agents discover their optimum policy by communicating with this environment and balancing their search between new actions and known rewarding behaviors.
- Exploration: The process of trying new actions leads to reward discovery.
- Exploitation: Agents choose rewarding actions that give known high outcomes through exploitation.
The model-free reinforcement learning methods approximate MDP solutions even when the environmental transition parameters and reward schemes remain unknown ahead of time.
The three main reinforcements learning algorithms DQN and PPO along with Actor-Critic methods structure their operation foundationally on MDP principles.
Conclusion
Reinforcement learning exists as a built framework on Markov Decision Processes known as MDPs. MDPs offer an advanced modelling structure which enables the analysis of decision processes in changing unpredictable situations. Studying MDPs provides comprehension of how intelligent agents learn optimal behaviour during the course of time.
MDP framework presents all fundamental learning and decision-making aspects beginning with state and action definitions and reward concepts and continuing through value functions and policy terms and model-based planning concepts. The MDP framework demonstrates widespread practicality because robotic systems and financial services along with healthcare solutions and gameplay applications all use its principles.
On-going development activities involving MDPs extend their scope of practical use while addressing known restrictions.
Reinforcement learning advancements make MDPs fundamental knowledge that every practitioner must master. SF students pursuing AI system development or interested in smart decision-making need to master Markov Decision Processes first.
FAQs
1. What is a Markov Decision Process (MDP) and why is it important?
An MDP is a mathematical framework for modeling sequential decision-making problems where outcomes are partly random and partly under the control of a decision-maker. It forms the foundation of reinforcement learning (RL) and is essential for understanding how agents learn optimal strategies in uncertain environments.
2. What are the core components of an MDP?
An MDP is defined by a 5-tuple:
- S: Set of states
- A: Set of actions
- P: Transition probability function P(s’|s,a)
- R: Reward function R(s,a,s’)
- γ: Discount factor that balances immediate vs. future rewards
3. What is the Markov Property and why does it matter?
The Markov Property states that the future state depends only on the current state and action not on the sequence of previous events. This property simplifies the modeling and computation of decision processes, making MDPs mathematically tractable and efficient to use in RL systems.
4. How are MDPs solved in practice?
MDPs are solved using several approaches:
- Dynamic Programming (DP) for known models
- Monte Carlo methods for sampling-based estimation
- Temporal Difference (TD) Learning, which blends both techniques
- Q-Learning and SARSA for model-free environments
5. What are some real-world applications of MDPs?
MDPs are used in a variety of domains:
- Healthcare: Personalized treatment and resource optimization
- Finance: Portfolio management and risk analysis
- Gaming: AI decision-making in games like AlphaGo
- Operations: Inventory and supply chain optimization
- Autonomous Vehicles: Navigation and hazard response