Difference between Linear Regression and Logistic Regression?
 Naveen
Naveen- 0
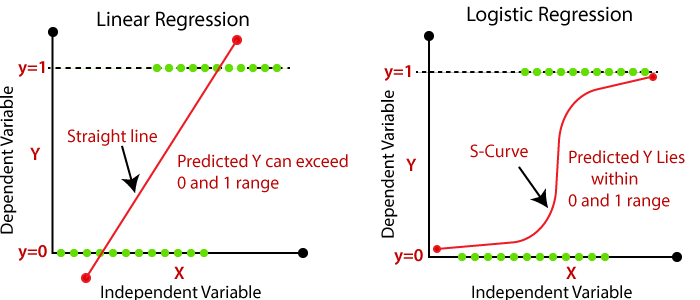
Linear regression and logistic regression are two of the most commonly used statistical techniques in machine learning and data analysis. Although both methods are used to predict outcomes, they differ fundamentally in their implementation and assumptions. In this article, we discuss the differences between linear and logistic regression.
What is regression?
Regression analysis is a statistical method used to determine the relationship between one or more independent variables and a dependent variable. The main purpose of regression analysis is to predict the value of the dependent variable based on the values of one or more independent variables. Regression analysis is widely used in machine learning, data science and other fields where data analysis is a critical aspect.
Linear regression
Linear regression is a type of regression analysis used to determine the linear relationship between a dependent variable and one or more independent variables. In linear regression, the relationship between the dependent variable and the independent variables is assumed to be linear. The purpose of linear regression is to find the line of best fit that represents the linear relationship between the dependent variable and the independent variable.
Applications of Linear Regression
Linear regression is widely used in various fields for prediction and forecasting. Some of the more common applications of linear regression include:
- Predicting stock prices
- Estimating sales revenue
- Forecasting weather patterns
- Estimating housing prices
- Analyzing the relationship between variables
Assumptions of Linear Regression
Linear regression has a number of assumptions that must be met to make accurate predictions. These assumptions include e.g.
- Linearity: The relationship between the dependent variable and the independent variables should be linear.
- Independence: Observations should be independent of each other.
- Homoscedasticity: The error variance must be constant for all values of the independent variables.
- Normality: The residuals should be normally distributed.
Logistic regression
Logistic regression is a type of regression analysis used to predict binary outcomes. In logistic regression, the dependent variable is binary, meaning that it can have only two possible values. Logistic regression is used when the dependent variable is categorical rather than continuous.
Applications of logistic regression
Logistic regression is widely used in various fields to solve binary classification problems. Some of the more common applications of logistic regression include:
- We predict whether a customer will buy a product or not
- Determine whether the patient has a certain disease or not
- Spam detection
- Determine if a credit card transaction is fraudulent or not
Assumptions of logistic regression
Logistic regression has a number of assumptions that must be met to produce accurate predictions. These assumptions include e.g.
- Independence: Observations should be independent of each other.
- Logit Linearity of Continuous Variables: The relationship between the logit of the independent variable and the logit of the dependent variable should be linear.
- Lack of multicollinearity: There should be no correlation between independent variables.
- Large sample size: The sample size should be large enough to ensure stable estimates.
Differences between linear and logistic regression
Outcome variable
The main difference between linear and logistic regression is the type of outcome variable. Linear regression is used when the dependent variable is continuous, while logistic regression is used when the dependent variable is binary.
Linearity
In linear regression, the relationship between the dependent variable and the independent variables is assumed to be linear. Logistic regression, on the other hand, assumes that the relationship between the independent variable and the dependent variable is linear.
Interpretation of coefficients
In linear regression, the coefficients of the independent variables represent the change in the independent variable with a unit change in the independent variable. In logistic regression, the coefficients represent the log-likelihood change in the independent variable given a unit change in the independent variable.
Residuals
In linear regression, the residuals are assumed to be normally distributed with constant variance across all values of the independent variables. In logistic regression, the residuals are not normally distributed and their variance is not constant.
Model performance
Linear regression is used to predict continuous variables and is estimated using measures such as mean square error (MSE) or root mean square error (RMSE). Logistic regression, on the other hand, is used for binary classification and is evaluated using metrics such as precision, accuracy, recall, and F1 scores.
Complexity
Linear regression is a relatively simple model that is easy to interpret and understand. Logistic regression, on the other hand, is a more complex model that requires more interpretation and understanding.
Use cases
Linear regression is used when the goal is to predict a continuous variable, while logistic regression is used when the goal is to predict a binary outcome.
Conclusion
In summary, linear regression and logistic regression are two statistical techniques widely used in machine learning and data analysis. Although both methods are used to predict outcomes, they differ fundamentally in their implementation and assumptions. Understanding the differences between linear and logistic regression is essential to choosing the right model for a given problem.
Popular Posts
Author
-

Naveen Pandey has more than 2 years of experience in data science and machine learning. He is an experienced Machine Learning Engineer with a strong background in data analysis, natural language processing, and machine learning. Holding a Bachelor of Science in Information Technology from Sikkim Manipal University, he excels in leveraging cutting-edge technologies such as Large Language Models (LLMs), TensorFlow, PyTorch, and Hugging Face to develop innovative solutions.
View all posts
